Planetary Orbital Parameters Explained: A Complete Glossary
Last Updated: October 13, 2023
Space is fascinating. Stars, planets, moons, asteroids and comets seem to just happily spin around in the void for aeons. Their orbits are finely determined by the very intricate influences from gravity fields that each planet of the solar system generates.
New discoveries are surprising scientists on a weekly basis and some of the things that happen in outer space are just radically challenging many of the things we know about the world.
Despite the ever-changing nature of space, there are some constants. Some things that we have studied extensively, understood for a long time, and now mastered completely. And one of those things is orbital mechanics.
Gravity is king in space, it collapses gigantic amounts of matter into an ignited star. It turns leftover material into planets and creates moons when said planets bump into each other.
Understanding gravity is important because it is the number one factor that influences the orbit of any floating object in space. Our understanding of gravity over the last 50 years has become so good that we now use it to boost our uncrewed spacecraft to whizz around the solar system at speeds we could not achieve with current technology (namely the “gravity assist” technique).
Whilst this topic should be its own article really, I thought it’d be an interesting introduction for my glossary of terms dedicated to planetary orbital parameters.
Orbital parameter's key data points
The below orbital parameters are used to describe the motion of natural and artificial objects in space, including planets, moons, asteroids, comets, and spacecraft.
Semimajor axis
The semimajor axis is half the longest diameter of an elliptical orbit. It represents the average distance between the celestial body and the object it orbits (usually the Sun for planets). It’s a useful measure because Planets don’t travel in perfect circles around their stars; their orbits are more elliptical.
To visualize this, imagine you have an oval drawn on a piece of paper. The longest diameter of the oval is called the major axis, and the shorter one is called the minor axis. The semimajor axis is just half of the major axis – it’s the distance from the center of the oval to the farthest point of the oval along the major axis. This gives us a good idea of the “average” distance throughout the planet’s orbital journey.
Sidereal orbit period (years)
The term “sidereal” comes from the Latin word “sidus,” which means “star.” In the context of orbits, it is used to describe measurements made with respect to the stars, as opposed to those made with respect to the Sun or other celestial bodies.
In the case of planets in our solar system, the sidereal orbit period is the time it takes for a planet to travel once around the Sun relative to the fixed stars. Since the stars are so far away, they essentially serve as a fixed reference frame.
For example, Earth’s sidereal orbit period is approximately 365.256 days (about one year). This is slightly different from the tropical year (approximately 365.242 days), which is the basis for our calendar year and is defined by the time it takes for the Sun to return to the same position in the sky as observed from Earth.
This data is useful for understanding the motion of celestial objects and predicting their positions in the sky.
Interesting fact: Some celestial bodies in our solar system have sidereal orbit periods that exhibit an interesting phenomenon called orbital resonance. In this case, the orbit periods of two or more objects are related by a simple integer ratio. For example, the orbits of Neptune and Pluto are in a 3:2 resonance, meaning that for every three orbits Neptune completes, Pluto completes two.
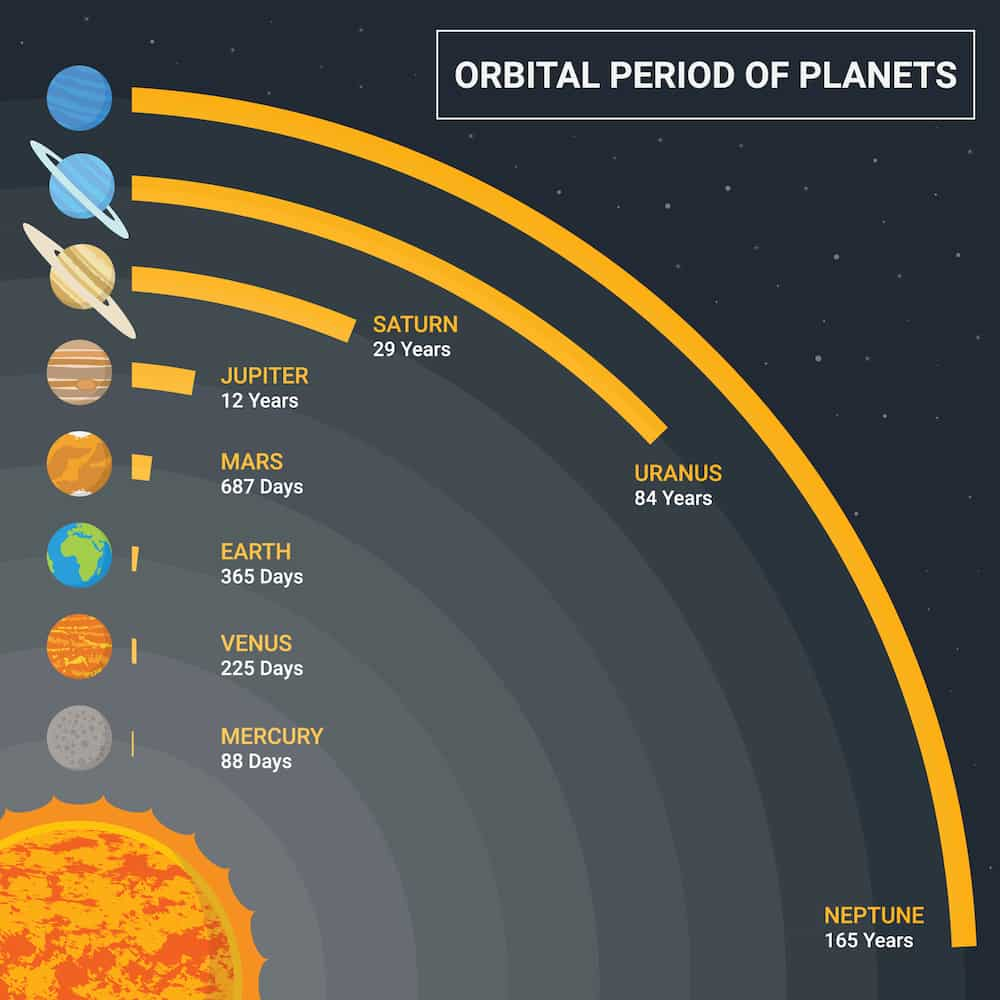
Tropical orbit period (days)
A tropical year is the time it takes for the Sun, as seen from the Earth, to return to the same position along the ecliptic (its path among the stars), particularly from one vernal equinox to the next. The vernal equinox is the point at which the Sun crosses the celestial equator (the projection of Earth’s equator onto the sky) moving from south to north.
This concept is significant because it corresponds closely to the cycle of seasons. The length of the tropical year is approximately 365.2422 days. This figure is slightly less than the 365.25 days of the average calendar year, which is why we have a leap year every four years (with some exceptions) to keep our calendar in sync with the seasons.
- Mercury: 87.969
- Venus: 224.695
- Earth: 365.2422
- Mars: 686.973
- Jupiter: 4,330.595
- Saturn: 10,746.94
- Uranus: 30,588.740
- Neptune: 59,799.9
Perihelion
The closest distance between a celestial body and its parent object (usually the Sun for planets) during its orbit. The term “perihelion” comes from the Greek words “peri,” meaning “near,” and “helios,” meaning “Sun.”
Celestial objects, such as planets or comets, experience stronger gravitational forces when they are closer to the Sun, causing them to move faster at perihelion than at any other points in their orbit.
Unsurprisingly, Mercury holds the crown to the smallest perihelion distance since it is the closest planet to the Sun. See the full list below:
- Mercury: 46 million km (29 million miles)
- Venus: 107 million km (66 million miles)
- Earth: 147 million km (91 million miles)
- Mars: 206 million km (128 million miles)
- Jupiter: 740 million km (460 million miles)
- Saturn: 1.35 billion km (839 million miles)
- Uranus: 2.74 billion km (1.7 billion miles)
- Neptune: 4.46 billion km (2.77 billion miles)
Interesting facts: Some comets such as the upcoming C/2023 A3 (Tsuchinshan-ATLAS) Comet, have highly eccentric orbits that bring them very close to the Sun at perihelion, causing them to develop spectacular tails as their volatile substances vaporize and stream off into space.
Aphelion
Aphelion is indeed the point in the orbit of a planet, asteroid, or comet at which it is furthest from the Sun. This term comes from the Greek words “apo” meaning away, and “Helios” meaning Sun.
When a planet is at aphelion, it is moving at its slowest speed and receives the least amount of sunlight, because it is at its maximum distance from the Sun. This contrast with the perihelion, which is the point in the orbit where the object is closest to the Sun, moving at its fastest speed, and receiving the most sunlight.
For example, Earth reaches aphelion in early July, when it’s about 94.5 million miles (152.1 million kilometers) from the Sun. In contrast, it reaches perihelion in early January, when it’s about 91.4 million miles (147.1 million kilometers) from the Sun.
Interesting fact: The difference between aphelion and perihelion distances is due to the fact that most orbits in our solar system are not perfect circles but ellipses, meaning they’re slightly squashed circles.
- Mercury: 0.47 AU / 69.8 million km / 43.4 million mi
- Venus: 0.72 AU / 108.9 million km / 67.7 million mi
- Earth: 1.02 AU / 152.1 million km / 94.5 million mi
- Mars: 1.67 AU / 249.2 million km / 154.9 million mi
- Jupiter: 5.46 AU / 816.6 million km / 507.4 million mi
- Saturn: 10.12 AU / 1.5 billion km / 934.5 million mi
- Uranus: 20.11 AU / 3 billion km / 1.86 billion mi
- Neptune: 30.33 AU / 4.54 billion km / 2.82 billion mi
Synodic period (days)
The synodic period is the time it takes for the object to reappear at the same point in the sky, relative to the Sun, as observed from Earth. This period differs from the sidereal period, which is the time it takes for the object to make one full orbit, relative to the stars.
The synodic period is especially important when considering the planets in our solar system. For instance, the synodic period of Mars is approximately 780 days. This means that approximately every 780 days, Mars and the Sun appear at the same point in the sky as seen from Earth.
- Mercury: Approximately 116 days
- Venus: Approximately 584 days
- Earth: Not applicable (Earth does not have a synodic period relative to itself)
- Mars: Approximately 780 days
- Jupiter: Approximately 399 days
- Saturn: Approximately 378 days
- Uranus: Approximately 370 days
- Neptune: Approximately 367 days
- Pluto (dwarf planet): Approximately 366 days
Mean orbital velocity (km/s)
The average speed of a celestial body along its orbit around the parent object, usually in kilometers per second (km/s).
- Mercury: 47.87 km/s
- Venus: 35.02 km/s
- Earth: 29.78 km/s
- Mars: 24.07 km/s
- Jupiter: 13.07 km/s
- Saturn: 9.69 km/s
- Uranus: 6.81 km/s
- Neptune: 5.43 km/s
Interesting fact: Compared to the inner planets, the outer planets orbit more slowly for two main reasons: they’re farther from the Sun, so the Sun’s gravitational pull is weaker, and they have a larger distance to cover to complete one orbit.
Max. orbital velocity (km/s)
The highest speed a celestial body reaches during its orbit around the parent object, usually in kilometers per second (km/s). Planets tend to reach their maximum orbital speed when they get closer to the Sun (at their perihelion).
- Mercury: 58.98 km/s
- Venus: 35.26 km/s
- Earth: 30.29 km/s
- Mars: 26.50 km/s
- Jupiter: 13.72 km/s
- Saturn: 10.18 km/s
- Uranus: 7.11 km/s
- Neptune: 5.50 km/s
Min. orbital velocity (km/s)
The lowest speed a celestial body reaches during its orbit around the parent object, usually in kilometers per second (km/s). Planets usually reach their lowest speed when they are located at their furthest point from the sun (at their Aphelion).
- Mercury: 38.86 km/s
- Venus: 34.79 km/s
- Earth: 29.29 km/s
- Mars: 21.97 km/s
- Jupiter: 12.44 km/s
- Saturn: 9.23 km/s
- Uranus: 6.52 km/s
- Neptune: 5.37 km/s
Orbit inclination (deg)
Orbital inclination refers to the tilt of an object’s orbit around the Sun (or another celestial body) compared to a reference plane. For planets in our solar system, this reference plane is usually the plane of Earth’s orbit around the Sun, known as the ecliptic plane.
Inclination is measured in degrees from this reference plane. An inclination of 0 degrees means the object’s orbit lies exactly in the reference plane. An inclination of 90 degrees would mean the object’s orbit is perpendicular to the reference plane.
For the planets in our solar system, their orbital inclinations are relatively small, meaning their orbits are nearly in the same plane. This is due to the way the solar system formed from a rotating disk of gas and dust.
However, other objects in the solar system, like asteroids, comets, or dwarf planets, can have much larger inclinations, with some even having ‘retrograde’ orbits that go in the opposite direction of the planets.
- Mercury: 7.00 degrees
- Venus: 3.39 degrees
- Earth: 0.00 degrees (by definition)
- Mars: 1.85 degrees
- Jupiter: 1.30 degrees
- Saturn: 2.49 degrees
- Uranus: 0.77 degrees
- Neptune: 1.77 degrees
- Pluto (dwarf planet): 17.16 degrees
Orbit eccentricity
A measure of the deviation of a celestial body’s orbit from a perfect circle. A value of 0 represents a circular orbit, while values closer to 1 indicate a more elongated orbit.
Interesting fact: At a value of 0.2056, Mercury has the most eccentric orbit than any other planet in the solar system.

Sidereal rotation period (hrs)
The time it takes for a celestial body to complete one rotation around its axis as measured relative to the background stars. This is expressed in Earth hours.
The term “sidereal” comes from the Latin word “sidus,” which means star. A sidereal rotation period is essentially a measure of how long it takes for a celestial body to rotate once relative to the distant stars.
This is an important parameter for understanding the rotational dynamics of astronomical objects, as it gives information about their internal structure, the distribution of mass, and the forces acting upon them.
Interesting fact: The sidereal rotation period of the Moon is about 27.3 Earth days, which is also the time it takes the Moon to orbit the Earth once. This is why we always see the same side of the Moon from Earth, a phenomenon known as tidal locking or synchronous rotation.
Length of day (hrs)
The time it takes for a celestial body to rotate once around its axis as observed from the parent object (usually the Sun for planets). This is expressed in Earth hours.
How does the planet stack up against each other? In order from the shortest day to the longest, we have:
- Jupiter at 9.93 hours or 9 hours and 55.8 minutes
- Saturn at 10.7 hours or 10 hours and 42 minutes
- Neptune at 16 hours
- Uranus at 17.23 hours or 17 hours, 14 minutes
- Earth at about 24 hours
- Mars at 24.6 hours
- Mercury at about 59 Earth days to turn once on its axis and about 176 Earth days for 1 full day-night cycle
- Venus at 243 Earth days
Interesting facts: At 243 earth days, Venus has the highest sidereal rotation period in the solar system. Moreover, Venus only takes 224.7 days to orbit the Sun, so basically a day on Venus is longer than a year on Venus!
Learn more: Planetary Time: How long is a day on each planet and Why?
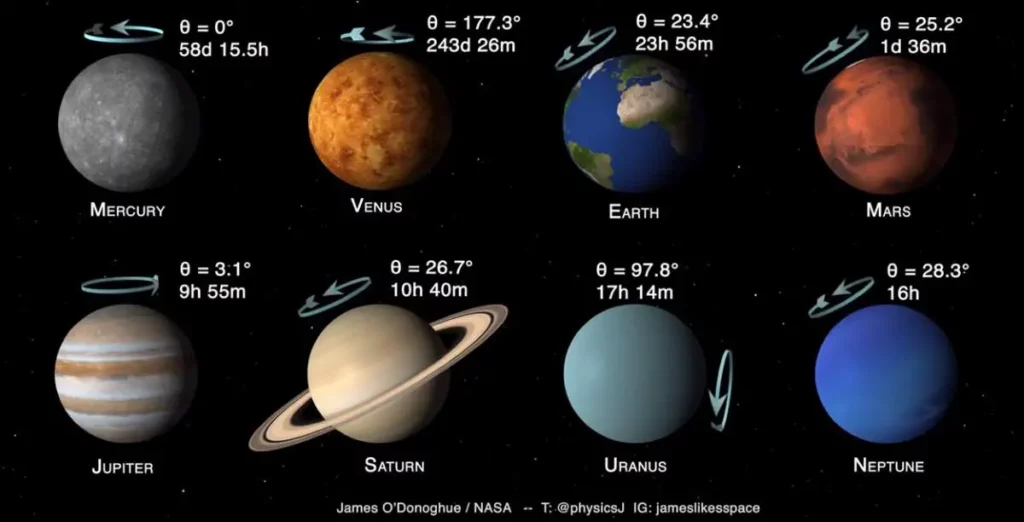
The obliquity to orbit (deg)
Obliquity to orbit refers to the angle between a celestial body’s rotational axis and a line perpendicular to its orbit. In simpler terms, it refers to the tilt of a planet’s or other celestial body’s axis of rotation in relation to the plane of its orbit around its parent body.
For example, the Earth has an obliquity of about 23.5 degrees, which means that the plane of its orbit around the Sun is tilted by that angle relative to the plane of its equator. This tilt is responsible for the seasons on Earth, as different parts of the planet receive varying amounts of sunlight depending on their orientation towards the Sun.
The obliquity of an orbit can have important consequences for the climate and habitability of a planet or moon, as well as for the dynamics of its orbit and its interactions with other objects in the solar system.
The inclination of the equator (deg)
The angle between a celestial body’s equator and a reference plane, typically the plane of the ecliptic (the plane in which Earth orbits the Sun). This is expressed in degrees.
For example, the Earth’s equator is inclined by about 23.5 degrees relative to the plane of its orbit around the Sun. This inclination is responsible for the fact that the Sun’s position in the sky changes throughout the year, which affects the length of daylight and the temperature in different regions.
The inclination of an equator can also have important consequences for a planet’s climate and the distribution of its biomes, as well as for its rotational stability and the dynamics of its atmosphere and oceans.
Interesting fact: Uranus’ equator is inclined at an angle of approximately 97.8 degrees relative to its orbital plane around the Sun. This means that the axis of rotation of Uranus is almost parallel to the plane of its orbit, resulting in extreme seasonal variations.
Why are orbital parameters important and who needs them?
Whilst I have focused on orbital parameters that pertain more specifically to planets so far, some of these factors (and more) are also used to analyse the orbit of other objects in space, namely comets, asteroids, satellites, and space stations.
Satellite tracking
As more satellites are launched into orbit, and with the increasing number of space junk, the risk of collisions also increases. This has become a major concern for space agencies, satellite operators, and scientists alike, as a collision could not only destroy expensive equipment but also create a cascade of space debris, potentially leading to a scenario known as the Kessler Syndrome.
Asteroid tracking
Additionally, understanding orbital mechanics is important for asteroid discovery and tracking. Observations over time allow astronomers to calculate an asteroid’s orbit and predict its future path. With this information, scientists can assess whether an asteroid poses a potential threat to Earth and monitor it more closely if necessary.
There are several programs and initiatives dedicated to finding, cataloguing, and tracking Near-Earth Objects (NEOs), which include asteroids and comets whose orbits bring them within 1.3 astronomical units (AU) of the Sun. Examples include NASA’s Near-Earth Object Observations (NEOO) Program and the International Asteroid Terrestrial-impact Last Alert System (ATLAS).
Space Station Navigation
There are currently two active space stations orbiting our planet. The ISS orbits the Earth at an altitude of approximately 400 kilometers (250 miles), traveling at a speed of around 28,000 kilometers per hour (17,500 miles per hour). It has to maintain a precise orbit to ensure the safety of the crew and the ongoing scientific experiments onboard.
Over time, the ISS experiences drag from the thin atmosphere at its altitude, which causes it to slowly lose altitude. To counteract this, periodic “reboost” maneuvers are performed which push the ISS to a higher orbit. If a piece of space debris is predicted to come within a certain distance of the ISS, a Debris Avoidance Maneuver (DAM) may be performed to change the station’s orbit and avoid a potential collision.
When spacecraft are sent to the ISS (carrying supplies or new crew members, for instance), precise navigation and understanding of orbital mechanics are essential to ensure a safe rendezvous and docking. Finally, When the ISS is decommissioned, its descent and reentry into the Earth’s atmosphere must be carefully controlled in order to reach its final resting place: the spacecraft cemetery.
Space mission planning
Reaching other celestial bodies far out in the solar system is no easy feat. Mastering orbital parameters is crucial in astronautics and in planning outer space missions, such as those involving spacecraft rendezvous, planetary flybys, or landing on other planets. Without knowledge of the precise orbits of celestial bodies, planning these missions would be impossible.
In the last 50 years, gravity assist maneuvres have been more commonly used to help speed up spacecraft on their way to the far distant planets. These are techniques used to change the path and speed of a spacecraft by using the gravity of a planet or other celestial body. They require a precise understanding of orbital mechanics to execute correctly.
For missions traveling to other planets, the Hohmann Transfer Orbit or other more complex trajectories are used to minimize the amount of energy (and thus fuel) required for the trip. These calculations depend heavily on the orbital parameters of the Earth and the target planet.

I’ve been fascinated by space and astronomy from a very young age. When I’m not watching space-themed documentaries, movies or TV series, I spend most of my free time in my backyard admiring the planets and galaxies with my telescope.
Wow! There's more to read 🚀
This page is part of our collection of astronomy articles. If you enjoyed the read, then you’ll love the following articles.




From Earth to Saturn: An intriguing journey exploring the distance, time and logistics of interplanetary travel between Earth and the ringed planet.
